抽屉原理(抽屉原理的基本形式总结)
提升数学思维,每天进步一点点!
【内容概述】
抽屉原则的两种基本形式与简单应用,其中包括运用抽屉原则或着眼于极端情形的各种袋中取球问题.“抽屉”与“苹果”以较为明显形式给出的论证问题.
【典型问题】
挑战级数:★
1.在200位学生中,在同一个月过生日的最少有多少人?
[分析与解] 因为有12个不同的月份,20012=16……8,所以在同一月过生日的最少有16+1=17人.
挑战级数:★★
2.学校买来历史、文艺、科普3种图书若干本,每名学生从中任意借2本,那么最少在多少名学生中才一定有两人所借图书的种类完全相同?
[分析与解] 注意到,6名学生可以将所有的可能借一遍:
(历史,历史),(文艺,文艺),(科普,科普),(历史,文艺),(历史,科普),(文艺,科普) .
所以第7名同学不管他怎么借,都在这6种情况之列.
所以最少在7名学生中才一定有两人所借图书的种类完全相同.

挑战级数: ★★★
3.一次智力竞赛,试卷上出了10道选择题,评分标准为:每人有10分基础百思特网分,每答对一题加4分,答错一题扣1分,不答的题不加分也不扣分.为了要保证至少有3人得分相同,则最少有多少人参加竞赛?
[分析与解] 如果全部做对可以得到10+104=50分,全部做错将得到10-101=0分,那么是不是50~0分之间所有的分数都能得到呢?
注意到49,48,47,44,43,39这6种分数得不到,于是共有51-6=45种不同的得分.
如果每种分数都有2个人得到,则需90人,那么第91个人的分数一定在45种分数之列,这样就一定有3人得到的分数相同.
所以,为了保证至少有3人得分相同,则最少有91人参加竞赛.
挑战级数:★
4.盒子中有10个红球、10个白球和10个绿球,它们的大小都相同.如果闭上眼睛,一次最少要取出多少个才能保证其中必有3个颜色相同的球?
[分析与解] 闭上眼睛,最不利的情况,前6个,将3种颜色的球各取了2个,那么第7个取出的球不管是何种颜色,一定和某两个球的颜色相同.
所以一次最少要取出7个才能保证其中必有3个颜色相同的球.

挑战级数:★★
5.一个布袋里有大小相同颜色不同l的一些木球,其中红色的有10个,白色的有9个,黄色的有8个,蓝色的有3个,绿色的有1个.那么一次最少要取出多少个球,才能保证有4个颜色相同的球?
[分析与解] 我们知道取出3个红球,3个白球,3个黄球,3个蓝球,1个绿球,此时仍然没有4个相同颜色的球,取出了3+3+3+3+1=13个球.
但是取出第14个球时,不管这个球是红色、白色还是黄色的,都有3个球的颜色与其相同.
所以一次最少要取出14个球,才能保证有4个颜色相同的球.
挑战级数: ★★★
6.暗室里有红、绿、蓝、黄、白5种颜色的袜子各50只,为确保从室内取出l0双袜子(两只袜子颜色相同即为一双),那么应从室内取出袜子的最少只数是多少?
[分析与解] 我们知道取出红色5只,绿色5只,蓝色5只,黄色5只,白色3只,此时只有9双袜子,此时有5+5+5+5+3=23只袜子.
但是第24只袜子不管取的是颜色,都能与上面的袜子在拼成一双.
所以,最少应从暗室中取出24只袜子,保证其中必有10双袜子.

挑战级数: ★★★
7.黑色、白色、黄色、红色的筷子各有8根,混杂放在一起,黑暗中想从这些筷子中取出颜色不同的两双筷子.问最少要取多少根才能保证达到要求?
[分析与解] 我们知道如果有黑色8根,白色1根,黄色1根,红色1根,其中没有两双颜色不同的筷子.此时取出了8+1+1+1=11根筷子.
但是第12根筷子不管是何种颜色,都能凑出另一种颜色不同的筷子.
所以要保证取出的筷子中有颜色不同的两双,最少要取12根筷子.
挑战级数:★★
8.口袋内装有4个红球、6个黑球和8个白球,一次最少取出多少个球,才能保证至少有1个白球和1个黑球?
[分析与解] 如果开始取出8个白球,4个红色,此时有12个球,但是没有黑百思特网球,但是再取一个球一定是黑色的,满足题意.
所以,一次最少取出13个球,才能保证至少有1个白球和1个黑球.
挑战级数:★★
9.口袋中有红、黄、蓝3种颜色的玻璃球各50个,闭着眼睛最少要摸出多少个球,才能保证红球数与黄球数的和比蓝球数多,黄球数与蓝球数的和比红球数多,红球数与蓝球数的和比黄球数多?
[分析与解] 将一种颜色与另两种颜色作为两个抽屉,为了使另两种颜色球数多于第一种颜色,至少放入502+1=101个苹果(球),才能使有一个抽屉有多于50个苹果,这个抽屉只能是两种颜色的抽屉.
那么,至少要取出101个球才能保证任何一种颜色的小球都会小另两种颜色的数量和.
挑战级数: ★★★
10.圆桌周围恰好有90把椅子,现已有一些人在桌边就坐,当再有一人入座时,就必须和已就坐的某个人相邻,则已就坐的最少有多少人?
[分析与解] 我们知道每隔2个人坐1个人,这样就会造成上面的情况,这时已经坐入903=30人,并且易知少于30人时,不能保证题中的情况出现.
所以,已就坐的最少有30人.
挑战级数: ★★★
11.有1999个数,每个数为0或1,如果要求当把这些数以任意的方式排列在圆周上时,总能找到37个l连排在一起.那么其中最少有多少个数是1?
[分析与解] 1999(37+1)=52……23,至少有54个0,那么可将1分成53段,这样必定有1段有37个连续的1.
此时,有1999-54=1945个1.
所以,要保证题中叙述的成立,最少有1945个1.

挑战级数:★★★
12.有64只乒乓球放在18个盒子中,每个盒子最多放6只乒乓球.那么最少有几个盒子里的乒乓球数目相同?(每个盒子必须放入球,不可以存在空盒情况)
[分析与解] 最多可以使得6个盒子的乒乓球的只数不等,依次为1,2,3,4,5,6只,这6个盒子共有21只乒乓球,
6421=3……1,
这样18个盒子放入了213=63只球,剩下的1只不管放到那个盒中,如果这只盒子放有k个球,那么现在就有4个盒子中的球是k+1个.
所以最少有4个盒子里的乒乓球数目相同.
挑战级数:★★
13.在笔直的马路上,从某点起,每隔1米种有1棵树.如果把3块“爱护树林”的小牌分别挂在3棵树上,请说明:不管怎么挂,总有2棵挂牌的树,它们之间的距离以米为单
位度量是偶数.
[分析与解] 设3棵挂排的树距离同一点O的距离分别为a,b,c.
这3个数中至少有两个同是奇数或同是偶数.
因为 奇数-奇数=偶数,偶数-偶数=偶数.
所以这3个数中至少有两个数之差是偶数.
这就说明不管怎么挂,至少有两棵挂牌的树之间的距离是偶数.

挑战级数: ★★★
14.数学教师带领30名学生做游戏,师生每人都各自在一张纸上把自然数1至30写成一行,顺序由自己决定.然同学们将自己的纸条与老师所写的纸条相比,有几个数与师所写的位置相同,就可得几分.现在知道30名学生所得分数各不相同,请说明其中必有1名学生所写的纸条与老师自顺序完全相同.
[分析与解] 我们注意到,学生写出的数最少没有1个和老师的相同,最多30个数的顺序完全相同,那么这就要31种不同的分值,但是这31种分值都能取到吗?
注意到,29分这个分值是取不到的,因为不可能正好有29个数与老师所写数的顺序相同,有29个数的顺序相同,那么第30个数的顺序一定也相同.
所以只有30种分值,并且每个学生各不相同,那么这30个分值每种都有人得到,即一定有得到30分的学生,这名学生所写的纸条与老师自己的顺序完全相同.
挑战级数: ★★★
15.图20-1是一个l010的方格表,能否在方格表的每个格中填入l,2,3这3个数之一,使得每行、每列及两条对角线上的各数之和百思特网互不相同?
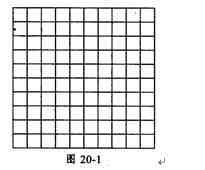
[分析与解] 不可能,因为每列每行每对角线上的和最小为10,最大为30.
10到30之间只有21个互不相同的整数值.而10行、10列及两条对角线上的各个数的和共有22个,所以这22条线上的各个数的和至少有两个是相等的.
