初等函数(基本初等函数的图像与性质)
在数学的发展过程中,形成了最简单最常用的六类函数,即常数函数、幂函数、指数函数、对数函数、三角函数与反三角函数,这六类函数称为基本初等函数。
一、常数函数
y = c 或 f ( x ) = c , x ∈ R ,其中 c 是常数。它的图像是通过点 (0,c),且平行 x 轴的直线,如下图所示:
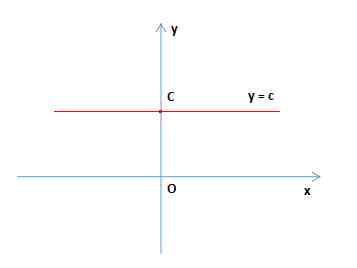
常数函数的图像
常数函数的性质:
1、常数函数是百思特网有界函数,周期函数(没有最小的正周期)、偶函数;
2、常数函数既是单调增加函数又是单调减少函数,特别的当 c = 0 时,它还是奇函数 。
二、幂函数
1、形如 y = x^a 的函数是幂函数,其中 a 是实数 。

幂函数图(1)
2、常见幂函数的图像:
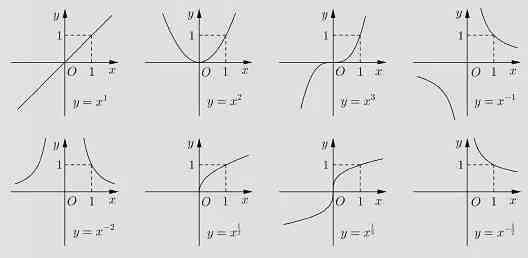
幂函数图(2)
注:画幂函数图像时,先画第一象限的部分,在根据函数奇偶性完成整个图像。
3、幂函数的性质:
① 幂函数的图像最多只能同时出现在两个象限,且不经过第四象限;如图与坐标轴相交,则交点一定是坐标原点 。
② 所有幂函数在 (0,+∞)上都有定义,并且图像都经过点 (1,1)。
③ 若 a > 0 , 幂函数图像都经过点 (0,0)和(1,1),在第一象限内递增;
若 a < 0 ,幂函数图像只经过点 (1,1),在第一象限内递减 。
三、指数函数
1、一般地,函数 y = a^x (a > 0 且 a ≠ 1)叫做指数函数,自变量 x 叫做指数,a 叫做底数,函数的定义域是 R 。
2、指数函数的图像:
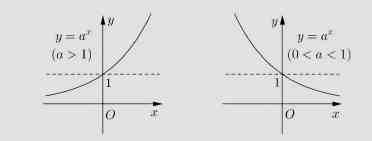
指数函数图象
3、指数函数的性质:
① 指数函数 y = a^x (a > 0 且 a ≠ 1)的函数值恒大于零 ,定义域为 R ,值域为 (0,+∞);
② 指数函数 y = a^x (a > 0 且 a ≠ 1)的图像经过点 (0,1);
③ 指数函数 y = a^x (a > 1)在 R 百思特网上递增 ,指数函数 y = a^x (0 < a < 1)在 R 上递减 。
四、对数函数
1、对数及其运算:
一般地,如果 a (a > 0 , a ≠ 1)的 b 次幂等于 N ,即 a^b = N,那么 b 叫做以 a 为底 N 的对数;
记作:logaN = b , 其中 a 叫做对数的底数, N 叫做真数 。
根据对数定义可知:
① 零和负数没有对数,真数大于零;② 1 的对数为 0 , 即 loga1 = 0 ;
③ 底的对数等于 1 ,即 logaa = 1 ;④ 对数恒等式:a^(logaN) = N 成立 。
通常以 10 为底的对数叫做常用对数,常用对数 log10N 简记作 lgN;
以无理数 e = 2.71828 ... 为底的对数叫做自然对数,自然对数 logeN 简记作 lnN 。
对数运算性质:如果 a > 0 , a ≠ 1 , M > 0 , N > 0 , 那么 :
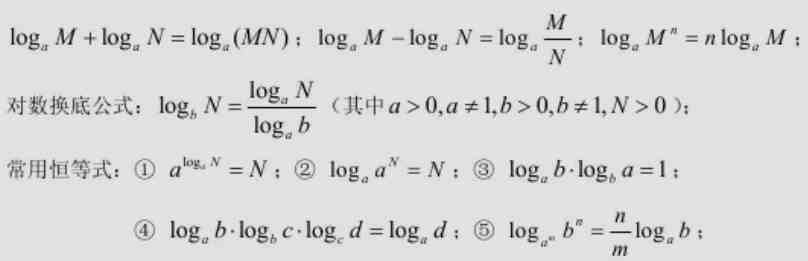
对数运算性质图
2、对数函数:
一般地,对数函数 y = logax (a > 0 且 a ≠ 1)就是指数函数 y = a^x (a > 0 且 a ≠ 1)的反函数。
因为指数函数 y = a^x (a > 0 且 a ≠ 1)的值域是 (0,+∞),
所以对数函数 y = logax (a > 0 且 a ≠ 1)的定义域是 (0,+∞)。
3、对数函数的图像:
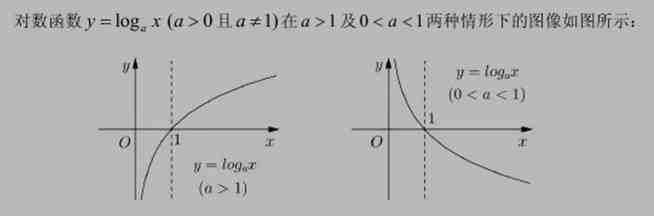
对数函数的图像
4、对数函数 y = logax (a > 0 且 a ≠ 1)的性质:
① 对数函数 y = logax (a > 0 且 a ≠ 1)的图像都在 y 轴的右侧,定义域是 (0,+∞),值域是 R ;
② 对数函数 y = logax (a > 0 且 a ≠ 1)的图像都经过点 (1,0);
③ 对数函数 y = logax (a > 1): 当 x > 1 时,y > 0 ;当 0 < x < 1 时,y < 0 ;
对数函数 y = logax&百思特网nbsp;(0 < a < 1): 当 x > 1 时,y < 0 ;当 0 < x < 1 时,y > 0 。
④ 对数函数 y = logax (a > 1)在 (0.+∞)上是增函数,
对数函数 y = logax (0 < a < 1)在 (0.+∞)上是减函数 。
五、三角函数与反三角函数
1、三角函数:y = sin x , y = cos x , y = tan x , y = cot x ;
2、反三角函数 : y = arcsin x , y = arccos x , y = arctan x , y = arccot x 。
3、三角函数的图像:
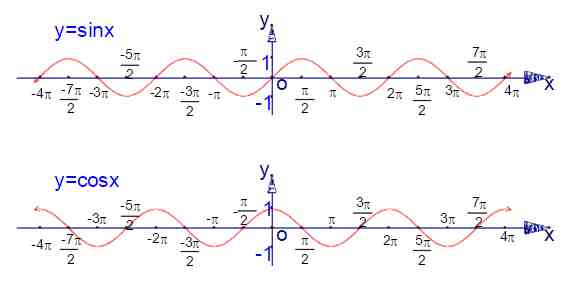
三角函数图像(1)
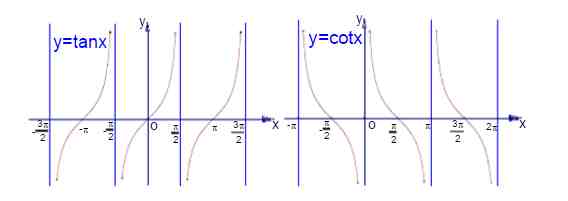
三角函数图像(2)
4、三角函数的性质:

三角函数的性质图
注:凡是由基本初等函数经过有限次的四则运算以及有限次的复合所生成的函数称为初等函数。
狄利克雷函数 D(x), 符号函数 sgn x ,整数函数 [ x ] 等都不是初等函数 。
欢迎关注头条号“尚老师数学”!
