析因设计(连续变量假设检验 之 析因设计方差分析)
在医学研究中,许多研究因素之间往往是相互联系的,相互百思特网制约的。当一个因素的质或量有改变时,其他因素的质和量也会随之改变。当几个因素间存在交互作用时,析因设计是一种非常理想的设计。
析因设计(Factorial Design)是将两个或多个因素的各个水平进行全面组合、交叉分组地设计,对各种可能的组合都进行实验,从而探讨各实百思特网验因素的主效应(Main Effect)以及各因素间的交互效应(Interaction)。
主效应是指某因素各单独效应的平均效应,即某因素各水平之间的平均差别,单独效应是指其他因素水平固定时,同一因素不同水平之间的差异。交互效应是指某因素的单独效应随着另一因素的水平变化而变化,则称这两个因素存在交互作用。也就是说析因分析不仅分析单个因素不同水平效应之间的差异,还要知道两个因素各水平间效应的相互影响。
常见析因设计有: 2x2析因设计、IxJ两因素析因设计、IxJxK三因素析因设计。
处理组数等于各因素水平之积,如两因素同时进行实验,每个因素取两个水平,实验总的组合数为22=4;若有3因素,每个因素取4个水平,实验总的组合数为444=64;下表有3个因素,各有2、2和3个因素,实验总的组合数为223=1百思特网2。
析因设计分析条件:由于方差分析要求资料的方差齐性,残差(residual)服从正态分布,故首先检验资料是否符合方差分析的条件。如果资料不满足方差分析的条件,可以先进行秩变换或其它的正态性变换(如Box-cox变换,对数变换,反正弦变换等),然后再做统计分析。
SPSS实现随机区组设计方差分析
示例:将20只家兔随机等分4组,每组5只,进行神经损伤后的缝合实验,欲比较不同缝合方法及缝合后时间对轴突通过率的影响。处理由两个因素组合而成,A因素为缝合方法,两个水平,水平一为外膜缝合,为a1,水平二维束膜缝合,为a2;B因素为缝合后的时间,两个水平,水平一为缝合后1月,为b1,水平二维缝合后2月,为b2;实验结果为家兔神经缝合后的轴突通过率(%)。数据如下所示。
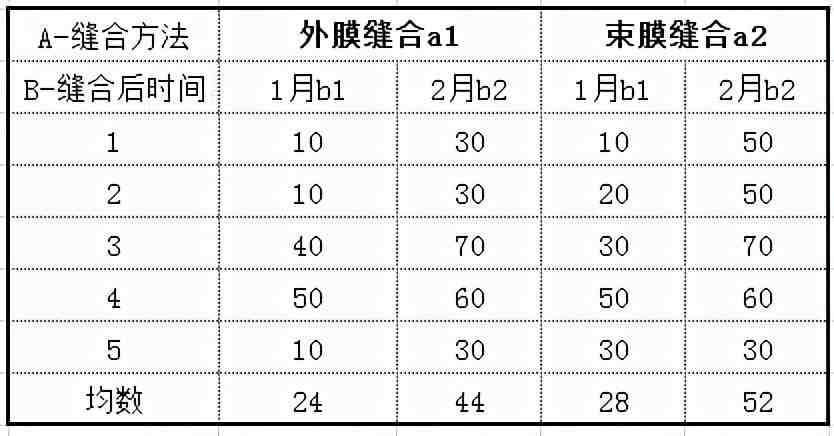
1. 示例分析:
本例研究2个因素A-缝合方法和B-缝合后时间,分别两个水平,全面组合,共构成4个单元,即4组,是一个22析因设计
2. 数据录入:
在SPSS的“变量视图”中设置三个变量,a代表缝合方法,数值型,有二个水平取值(1-外模缝合和2-束膜缝合);b代表缝合后时间,数值型(1-1个月,2-2个月);x代表通过率,数值型。
3. 建立假设:建立检验假设,确定检验水准
(1)因素A
H0: 不同缝合方法的通过率总体均数相等
H1: 不同缝合方法的通过率总体均数不相等
(2)因素B
H0: 不同缝合时间的通过率总体均数相等
H1: 不同缝合时间的通过率总体均数不相等
(2)交互作用A与B
因素A与B无交互作用
因素A与B有交互作用
= 0.05,即置信区间为95%
4. 析因设计方差分析简要
(1) 打开 分析—一般线性模型—单变量
(2) 参数选择
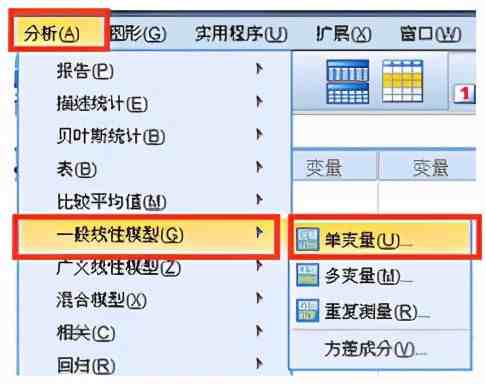
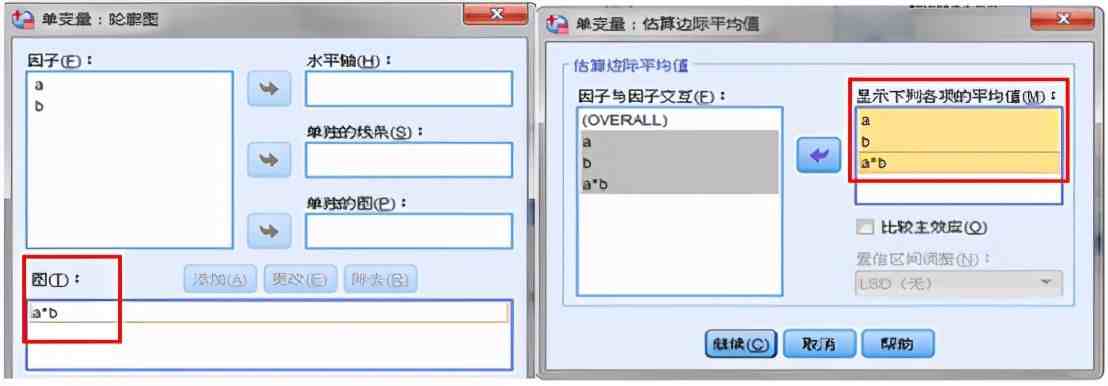
单变量主对话设置:如图A将x放入因变量,a 和b放入固定因子。
模型参数设置:点击“模型”,图B,因为本例为析因设计,因此需要分析交互作用,因此选择默认的“全因子”,点击“继续”返回。
图:a为水平轴,b为分组
EM平均值:选择a、b及a*b交互作用
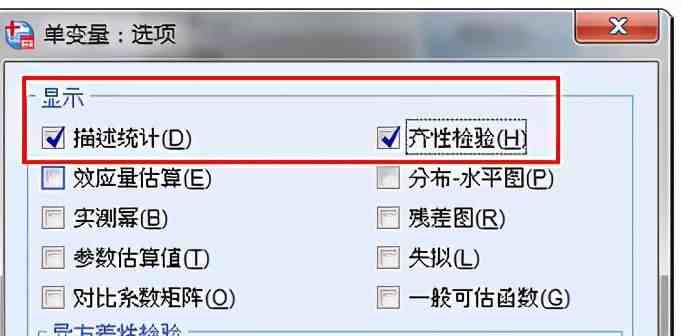
选项:显示勾选"描述统计”和“方差齐性”,点击“继续”
5. 数据结果与说明
(1) 输出样本量及相应均值

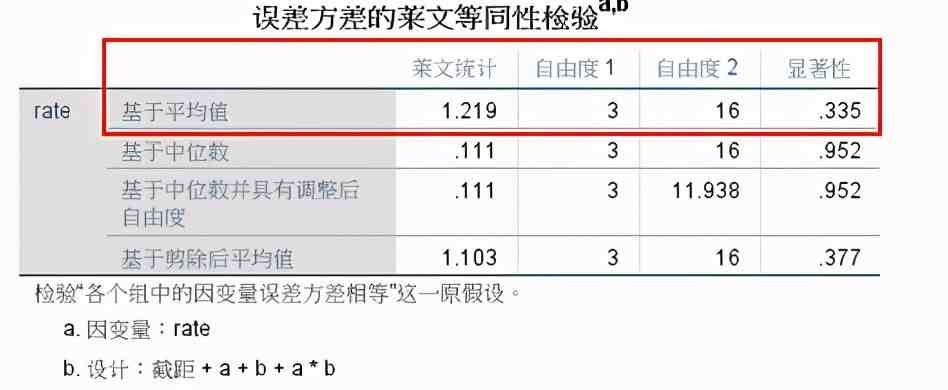
(2) 方差齐性检验:可见levene齐性检验F =1.219,P =0.335>0.05,各组方差齐,可以进行后续方差分析。
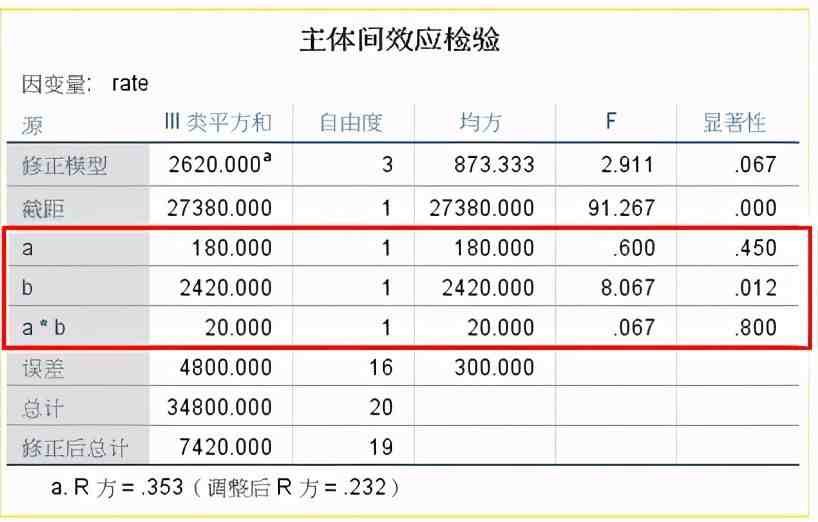
(3) 主体效应间比较:
缝合方法F=0.600,P=0.450,按照=0.05检验水准,不拒绝H0,差异无统计学意义,尚不能认为两种缝合方式间轴突通过率不同(A因素主效应≠0);
缝合后时间F=0.8607,P=0.012,按照=0.05检验水准,拒绝H0,接受H1,差异有统计学意义,可以认为不同时间轴突通过率不同(B因素主效应≠0);
缝合方法与缝合后时间交互F=0.067,P=0.800,按照=0.05检验水准,不拒绝H0,差异无统计学意义,尚不能认为缝合方式与时间存在交互作用(AB因素交互作用≠0)。
(4) 下图显示边际轮廓图,结果得到几乎相平行的直线,表示该研究两因素交互作用小。反之,若得到两条相互不平行的直线,则说明两因素可能存在交互作用。
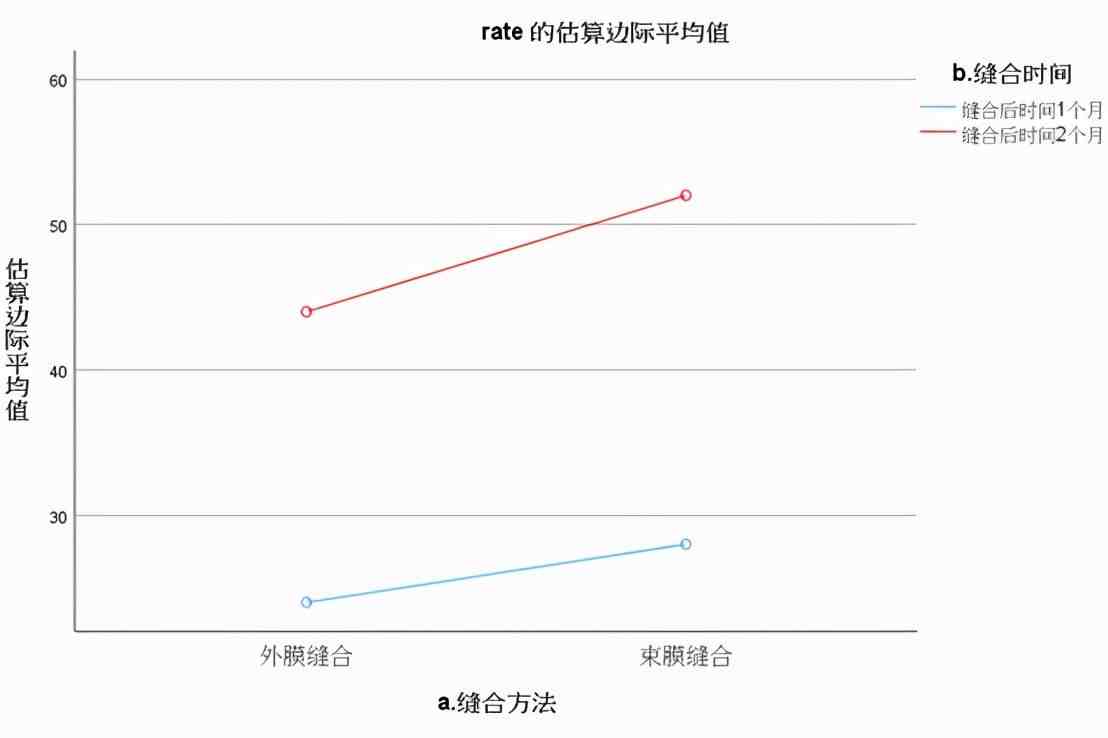
结论:不能认为两种缝合方法对通过率有影响,以及两个因素间存在交互作用。但可认为缝合后2个月与1个月相比,通过率提高了。
6. 语法
UNIANOVA rate BY a b /METHOD=SSTYPE(3) /INTERCEPT=INCLUDE /PLOT=PROFILE(a*b) TYPE=LINE ERRORBAR=NO MEANREFERENCE=NO YAXIS=AUTO /EMMEANS=TABLES(a) /EMMEANS=TABLES(b) /EMMEANS=TABLES(a*b) /PRINT DESCRIPTIVE HOMOGENEITY /CRITERIA=ALPHA(.05) /DESIGN=a b a*b.
