全等三角形难题（一道无从下手的全等三角形问题）

示例：如图，△ABC中，AD⊥BC于D，AB＋BD＝AC＋CD，求证：AB＝AC；

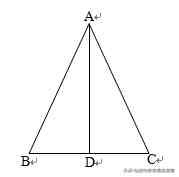
初看本题无从下手，仔细想一想本题已知AB＋BD＝AC＋CD，则需将AB、BD置于同一条线段上，AC、CD置于同一条线段上，因此如图所示，延长百思特网DB至E，使BE＝AB，延长DC至F百思特网，使CF＝AC.从而此时DE＝DF，又因为AD⊥EF百思特网，根据线段垂直平分线性质可知：AE＝AF→边及时联想到角可知∠E＝∠F.（不能忘了等边对等角可知∠E＝∠BAE，∠F＝∠CAF）

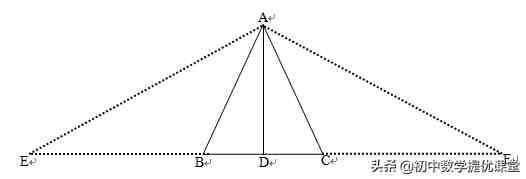
继续思考：要证AB＝AC可根据等角对等边（∠ABC＝∠ACB）实现AB＝AC，而∠ABC、∠ACB与∠E、∠F是外角的关系.

如图，由外角性质可知∠ABC＝∠E＋∠BAE＝2∠E，∠ACB＝∠F＋∠CAF＝2∠F；所以∠ABC＝∠ACB，∴AB＝AC.

总结：本题如果延长AB、AC将BD、CD转化的话就用不着AD⊥BC这个条件了，因此只能延长DB、DC.

反思：将出现两边之和等于另一条线段（或两边之和）要想到将不在同一条直线的两条线段放于同一边上.

本文来源于平时教学总结！