分数的基本性质教学反思(对“分数基本性质”的重新审视)
今天阅读了刘晓婷老师的《真问题驱动的教学反思》第三章课例式教学反思中的第4个课例“在把握基本思想中涉及学习问题——分数基本性质的研磨与思考”。其中感触最深的是刘老师在文中对“分数基本性质”的重新审视。百思特网
一、分数基本性质承上启下了什么?
分数基本性质是一堂承上启下的课,那么“上”承的是什么?“下”启的又是什么?
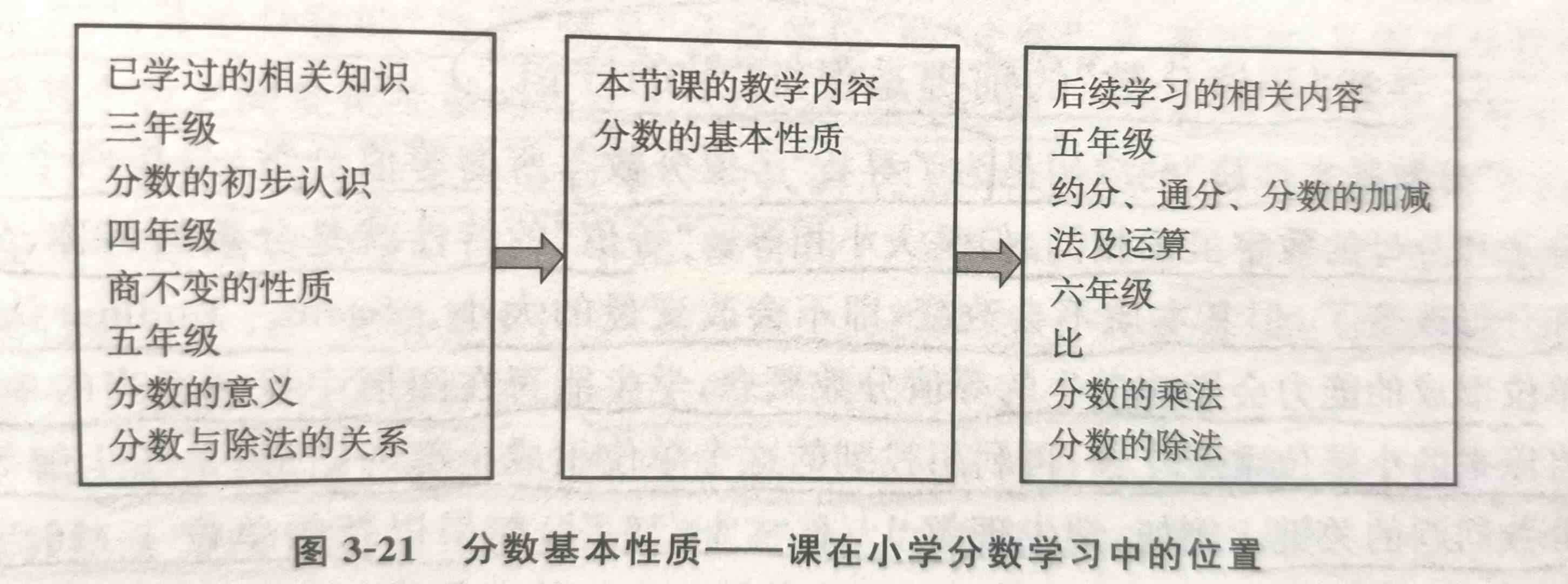
分数基本性质的承上启下,主要体现在以下几个方面:
(1)承上。联系分数与除法的关系,分数的基本性质与商不变的规律,事实上是从不同的形式表示相同的规律,分数的基本性质有助于学生对分数意义的进一步理解,加深对单位1的认识,在分子分母变化的同时,不变的是单位1。换句话说,在单位一不变的情况下,要保证分数的大小不变,分子分母要同时变化。
(2)启下。单纯分数这一内容来说,分数的基本性质是通分和约分的理论依据,根据分数的基本性质,我们能够解决分数单位的换算问题,统一分数单位,使一分母分数能够进行加减运算。

二、分数基本性质承上启下的核心在于分数单位。
分数单位作为分数的计数单位,他是后续所有后续知识,技能的基础,包括分数的意义,分数的基本性质,分数的大小比较约分,通分分数的加减法,分数的乘除法,以及有关分数的实际问题的解决。事实上,在数学发展史上,发现新的计数单位,始终是数的发展的一条主线。人们认识分数首先都是从认识分数单位开始的。
三、寻找“等值分数”的前提是保证“量的守恒”。
“分数基本性质”的应用是为了寻找“等值分数”,所谓“等值分数”是指两个分数分子和分母的数字虽不相同,但是大小相等,“等值”的特点就是分数名称,分子和分母变化了,但其本质百思特网不会改变,即不会改变量的大小。Saenz-Ludlow认为,分数单位形成的能力会影响学生的等值分数概念,学生能否在图形中找到适当的单位,将原来小的单位重新化聚,再利用找到的这个单位组成全部的图形,是学生解等值分数问题的关键。例如学生理解,1/4=40/16, 如果以新的单位1/16来看时,1/4部分就是4个1/16,所以可以说4/16, 从而得出1/4与 4/16一样大的结论,这就是单位形成能力。
这种单位形成能力,是以儿童守恒能力发展为前提的,守恒是皮亚杰理论当中的一个重要术语,是指物体的形式(主要是百思特网外部特征)起了变化,但是个体认识到物体的量(或内部性质)并未改变,之所以当分数单位即(分母)发生变化,分数大小还能保持不变,就是因为尽量分的份数多了,分数单位变小了,单位的个数(分子)却增多了,如果儿童不能够认识到这样一点,则无法真正理解等值分数和分数基本性质的内涵。

刘加霞教授指出,基于度量的需要,"数"分数单位的"个数",从而得到分数,体现出分数是个"数"(度量数) 的意义,沿袭自然数的传统,分数的两个关键要素就是"分数单位"、"单位个数",即分数单位的"分母"是平均分的份数,分子是1,其他分数的分子就是分数单位的个数,基于此要探寻分数单位及其个数之间的变化关系的角度来认识分数的基本性质,至少有以下几点好处。
(1)再次巩固了学生对分数单位的认识,尽管不同版本教材的处理略有不同,但在五年级分数意义这1单元都讲到了分数单位,在分数基本性质这一课中再次聚焦分数单位,以分数单位及其个数为主线来寻找等值分数,是对之前学习内容的进一步巩固。
(2)加深学生对分数是个“数”的理解,提升分数作为“代数概念”的价值,一直以来在学生心目中都不愿意承认“分数是个数”,更愿意把其理解为率,通过找到不同的分数单位,在数出其个数,并用结果来比较大小的过程,学生能进一步认可作为量的分数的概念。
(3)将分数置于度量范围之下去理解,为学生今后理解通分、约分、异分母分数加减法进行铺垫。
在"分数基本性质"教学中,如果能够以分数单位为主线,通过"度量"去寻找等值分数,将为后续理解通分、约分以及分数基本性质的应用奠定基础。

